Distortion of Signals in Analog Fiber-Optic Links with Direct and External Intensity Modulation
V.V. Shcherbakov1, A.F. Solodkov1, A.A. Zadernovsky2
1) JSC “Center VOSPI” Moscow, Russia info@centervospi.ru
2) Department of physics, Moscow Technological University, MIREA, Moscow, Russia zadernovsky@mirea.ru
This work was partially supported by Ministry of Education and Science of the Russian Federation.
I. INTRODUCTION
Fiber-optic links are widely used in various areas of science and technology. In the field of telecommunications, digital data transmission systems are mostly employed. However, the analog systems with intensity modulation (IM) of the light produced by a semiconductor laser, transportation of the optical signal through an optical fiber and, finally, direct detection (DD) of the optical signal by a photodiode at the output of the fiber, are in demand for a variety of applications.
There are two basic schemes for the light intensity modulation, which compete with regard to simplicity and performance. The first scheme uses direct intensity modulation, which can be achieved by varying the drive current of the semiconductor laser. Unfortunately, this current variation not only modulates the laser light intensity, but induces a parasitic optical frequency modulation, the effect which is referred to as laser chirp. Frequency chirp of laser light can cause degradation and harmonic distortions of the transmitted signals after propagation in a dispersive optical fiber.
The second scheme was proposed as a solution to the problem of chirp. This scheme uses external intensity modulation of the laser light by chirp-free electrooptic Mach-Zehnder modulator (MZM). However, the intensity modulation response of MZM is highly nonlinear and exhibits intrinsic harmonic distortions of the output optical signal. After propagation in a dispersive fiber this signal can acquire additional harmonic distortions.
In this paper we examine performance characteristics of the IM/DD fiber-optic links with direct and external intensity modulation. We present experimental results on signal transmission in these systems and compare the harmonic distortions of signals.
It is worth noting that in the majority of studies of IM/DD fiber-optic links, either numerical analysis [1, 2] or rather complicated mathematical apparatus [3] are usually used. This makes difficult obtaining the simple analytical expressions suitable for the engineering design of the fiber-optic links. This paper is intended to fill this gap. We present a simple analytical expression for the frequencies of the signals with minimum or with maximum power at the output of a fiber, as well as a simple analytical expression for the frequencies at which one can expect the minimum dispersive harmonic distortions.
II. EXPERIMENT
A. Direct intensity modulation
The experimental setup is shown in Fig. 1. The work procedure is as follows. The single-frequency 1550 nm DFB InGaAsP laser NLKC5EBKA (2) is connected to the input of photodetector U2t, XPDV2150R (3) by a short length of standard single-mode optical fiber (4) about 1 m long and then we determine visually on screen of the analyzer Agilent N5244A (1) the frequency range where the modulation response has no significant noise and sharp breaks. In this frequency range (in our case 10MHz - 35GHz) the signal power is normalized to unity. Then, the short cable (4) is replaced by a coil of long optical fiber (5) and the output signal is displayed on the screen of analyzer (1). Acting in a similar manner, we can get intensity modulation response for several lengths of a single-mode fiber. However, the laser light intensity should not be greater than 5-7 dBm because of the risk of stimulated Brillouin scattering and nonlinear distortions.
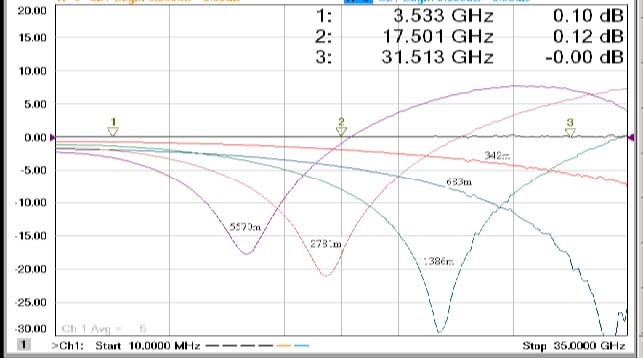
Fig. 2 shows the experimental curves for the output-to-input power ratio of the signals (expressed in dB) versus the modulation frequency fm for several coils of fiber of different length L with the dispersion coefficient D = 17 ps/(nm km).
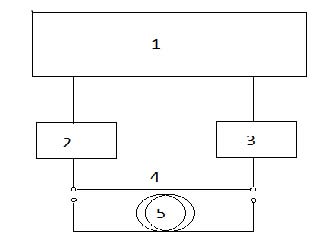 |
| Fig. 1. Experimental setup for measuring the intensity modulation response. |
|
|
| Fig. 2. Output-to-input signal power ratio (expressed in dB) versus the modulation frequency for several lengths of a single-mode fiber. |
B. Harmonic distortions.
Nonlinear distortions manifest themselves in generation of the harmonics that are not presented in the original signal. Figs. 3, 4 represent the observed relative power of the 2nd and the 3rd harmonics, respectively, (harmonic-to-carrier power ratio) versus the power of signal. We use two different sources of light. The first source is a directly modulated single-frequency 1550 nm DFB InGaAsP laser (in the figures it is referred to as N43), built-in Agilent N4373A analyzer. The second source is the laser with an external chirp-free MZM, which is not stabilized in the quadrature operating point (in the figures it is referred to as L340). The 2.2 GHz signal of modulation is generated by Agilent E5071B with the microwave filter to suppress the intrinsic harmonic distortions.
The optical signal is fed either directly to a photodetector Agilent N4373A, or through a coil of Corning fiber of 25266m length (in the figures it is referred to as AD-1). The power of harmonics in the output signal is measured by a spectrum analyzer Agilent E4404B in the segmented scanning mode.
III. THEORY
A. Direct intensity modulation
Theoretical interpretation of the experimental results includes the frequency chirp of directly modulated laser and the group velocity dispersion of electromagnetic waves in optical fiber. The frequencies of the power extrema in Fig. 2 are found to be equal
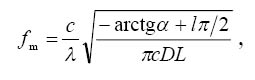 |
(1) |
where odd integers l give the minima, whereas even integers l give the maxima, λ is the carrier wavelength, c is the speed of light, α is the chirp parameter, also known as Henry factor and D is the dispersion coefficient of a fiber. The values of the signal power extrema are related with the laser-specific parameter k which is referred to as the adiabatic chirp coefficient. Unfortunately, laser vendors do not specify the chirp parameters. Applying the data presented in [4] (α=2.8±0.2, k = (11.4 ± 0.5) c-1 mW-1) we come to a good agreement between our experimental and theoretical results.
B. Harmonic distortions of directly modulated signals
The relative powers (Figs. 3, 4) of the 2nd and the 3rd harmonics of radiation of directly modulated laser N43 (with chirp) are extremely small and consist of less than -55 dBc and -70 dBc, respectively. Practically, the laser operates as a linear electrical-to-optical convertor. After the optical signal transportation through the 25266 m fiber, the powers of the 2nd and the 3rd harmonics are significantly increased by 34 dBc and 36 dBc, respectively, and this increase is independent of the power of signal. The latter demonstrates the nature of dispersive harmonic distortions, which are not associated with the optical power. The primary reason for the harmonic distortions is the frequency chirp of light produced by a directly-modulated laser and the group velocity dispersion of electromagnetic waves in a fiber. In linear propagation through a fiber the different spectral components of the chirped optical signal acquire different phase changes due to dispersion. This leads to appearance the higher order harmonics which are not presented in the original signal. We have obtained a simple analytical expression for the particular frequencies
|
|
(2) |
at which there will be no dispersive harmonic distortions for small modulation signals.
C. Harmonic distortions of externally modulated signals
When using the L340 laser source with an external chirp-free MZM, the inclusion into the optical circuit a fiber coil of 25266 m length practically does not change the relative powers of the higher order harmonics shown in Figs. 3, 4. Theoretical interpretation of this result takes into account the intrinsic nonlinearity of MZM.
The original signal of voltage modulation applied to MZM is a single-tone electrical signal. It is subjected to nonlinear distortions already at the stage of the electrical-to-optical conversion. And although by the choice of the quadrature bias one can eliminate the contribution of all even harmonics, and by the restriction of the modulation voltage amplitudes one can significantly reduce the contribution of higher order odd harmonics, the nonlinear distortions, caused by operation of MZM, are basically unavoidable.
After transportation through a dispersive fiber, the optical signal can acquire additional harmonic distortions. The photocurrent detected at the fiber output contains both even and odd harmonics of the modulation frequency despite the fact that at the quadrature operating point of MZM the fiber input optical signal contains no even harmonics. The signal output-to-input power ratio is determined by the fiber transportation parameter
| θ = πc(fm/f0)2DL | (3) |
where f0 is the carrier frequency. At the modulation frequencies, determined from the condition |cosθ| = 1, which yields θ = lπ with l = 0,1,2,3..., the modulus of the transfer function reaches the maximum value equal to unity and, thus, the optical powers of the fundamental and higher order harmonics in the input and in the output signals become equal to each other (without attenuation in the fiber).
In our experiment we have used a chirp-free MZM, which is not stabilized in the quadrature operating point and therefore we observe both even and odd harmonics at the input to the fiber. At 2.2 GHz modulation frequency we have |cosθ| ≈ 1, and, thus, the powers of the second and the third harmonics after propagation through the fiber are close to their powers at the fiber input. The harmonic distortions of the output signal in this case are entirely determined by the nonlinear properties of the MZM modulator.
IV. CONCLUSION
We have presented experimental and theoretical results on transmission of signals in analog IM/DD fiber-optic links with direct or external intensity modulation. We have experimentally obtained the intensity modulation response for several directly-modulated IM/DD fiber-optic links of different lengths. We have obtained a simple analytical expression for the frequencies of the signals with minimum or maximum power at the fiber output. We have specified the operation conditions of directly or externally modulated IM/DD fiber-optic links, ensuring minimum harmonic distortions of the transmitted signals. The results are useful for the engineering design of fiber-optic links.
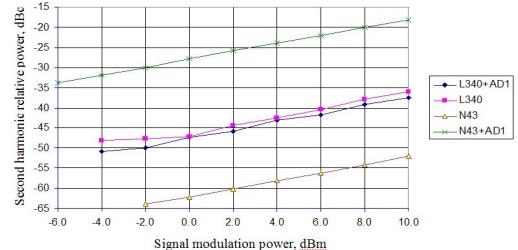 |
| Fig. 3. Relative power of the 2nd harmonic versus the power of signal |
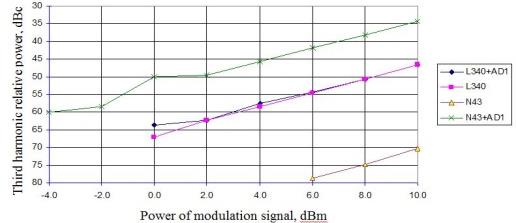 |
| Fig. 4. Relative power of the 3rd harmonic versus the power of signal |
V. REFERENCES
[1] G.J. Meslener, “Chromatic dispersion induced distortion of modulated monochromatic light employing direct detection,” IEEE J. Quantum Electron., vol. 20, pp. 1208-1216, 1984.
[2] A. Hilt, E. Udvary, T. Berceli, “Harmonic distortion in dispersive fiber–optical transmission of microwave signals,” Proceedings of International Topical Meeting on Microwave Photonics, pp. 151-154, 2003.
[3] E. Pera, A. Yariv, “Large-signal theory of the effect of dispersive propagation on the intensity modulation response of semiconductor lasers,” Journal of Lightwave Technology, vol. 18, pp. 84-89, 2000.
[4] A. Villafranca, J. Lasobras and I. Garcés, “Precise characterization of the frequency chirp in directly modulated DFB lasers,” Proceedings of 6th Spanish Conference on Electronic Devices, pp. 173-176, 2007.
Мы будем рады ответить на них!
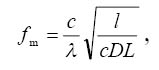 l = 1,2,3...
l = 1,2,3...