Дисперсионные искажения сигнала в аналоговых волоконно-оптических линиях связи с прямой модуляцией интенсивности

Введение

Волоконно-оптические линии связи (ВОЛС) получили самое широкое распространение в различных областях науки и техники. В области телекоммуникаций в подавляющем большинстве случаев используются цифровые системы передачи информации. Однако, простейшие аналоговые системы с прямой СВЧ модуляцией интенсивности излучения на входе (путем модуляции тока накачки инжекционного полупроводникового лазера), транспортировкой сигнала амплитудной модуляции несущей электромагнитной волны по оптоволокну и прямым детектированием фототока на выходе остаются востребованными для различных применений. Среди них, например, локальные волоконно-оптические сети специального назначения, позиционно разнесенные системы радиолокации, антенные системы, удаленные от пунктов управления и обработки информации и другие. При этом, использование именно аналоговых ВОЛС в таких системах часто оказывается не только безальтернативным, но и надежным и экономически выгодным решением.

Вместе с тем, у аналоговых ВОЛС есть существенные недостатки. К наиболее важным из них относятся нелинейные искажения и периодическая деградация сигнала (вплоть до уровня шума) по мере его транспортировки по волокну. Выбор оптимальных параметров схемы ВОЛС должен опираться на ясное понимание причин возникновения указанных недостатков. В большинстве работ, посвященных этой теме исследования, используются либо численный анализ, либо довольно сложный математический аппарат, затрудняющий, из-за сложности математических преобразований, получение простых аналитических выражений, пригодных для инженерного проектирования ВОЛС. Данная работа призвана восполнить этот пробел. Для этого мы рассмотрим последовательно все этапы прохождения сигнала в аналоговой ВОЛС. Сначала, преобразование входного электрического сигнала модуляции тока инжекции в оптический сигнал полупроводникового лазера. Затем, транспортировку оптического сигнала в одномодовом волокне с хроматической дисперсией и, наконец, обратное преобразование оптического сигнала в электрический при его прямом детектировании с помощью фотоэлемента на выходе из волокна.

 

Преобразование электрического сигнала в оптический сигнал

Прямая модуляция тока накачки инжекционного лазера является наиболее простым способом преобразования электрического сигнала в оптический. Динамические явления в излучении инжекционных лазеров при модуляции тока накачки подробно исследованы в [1, 2]. В современных инжекционных лазерах в частотном диапазоне модуляции до 30 ГГц такое преобразование происходит с минимальными нелинейными искажениями, а ватт-амперная характеристика в надпороговом режиме генерации при низких мощностях излучения хорошо описывается линейной функцией. Поэтому, гармонический электрический сигнал тока модуляции

,

(1)

где I₀ ‑ ток смещения, который выводит рабочую точку на линейный участок ватт-амперной характеристики и m – глубина модуляции, преобразуется в оптический сигнал модуляции мощности излучения лазера

(2)

с такой же циклической частотой ω_m и фазой φ_m.

Можно представить себе, что соответствующая электромагнитная волна излучения с частотой ω₀ и начальной фазой φ₀ будет модулирована следующим образом

.

(3)

Это выражение может быть разложено в ряд по m. Если при малых глубинах модуляции m0 ± ω_m, что характерно для амплитудной модуляции.

Следует отметить, что в (3) не учтен эффект частотного чирпа [3] ‑ возникновение фазовой (а следовательно и частотной) модуляции электромагнитной волны излучения лазера при модуляции тока накачки. Действительно, периодическое изменение концентрации неравновесных носителей при модуляции тока инжекции приводит к периодическому изменению показателя преломления активной области и, следовательно, к модуляции частоты лазерного излучения. Эффект частотного чирпа принято записывать в форме зависимости мгновенной частоты ω от мощности P лазерного излучения. А именно [3‑ 6],

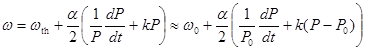(4)

где α называется фактором Генри, а k - коэффициентом адиабатического чирпа. Из (4) видно, что частота несущей волны излучения лазера в рабочей точке ватт-амперной характеристики равна ω₀ = ω_th + ( α / 2 ) kP₀ и отличается от частоты лазерного излучения на пороге генерации 

ω_th на величину (α / 2) ω_c, где ω_c = kP₀ называется характеристической частотой адиабатического чирпа. Вследствие чирпа фаза φ₀ в выражении для напряженности поля (3) уже не будет постоянной и должна быть заменена на функцию Φ(r), определяемую из соотношения

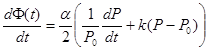(5)

Типичные значения параметров чирпа для InGaAsP лазеров с распределенной обратной связью (длина волны λ₀ = 1550 нм) таковы [5, 6]: α заключено в пределах от 2 до 4, а характеристическая частота адиабатического чирпа f_c = ω_c / 2π находится в пределах от 1 до 3 ГГц при мощности излучения P₀=1 мВт. .

Интегрирование (5) дает следующее выражение для фазы

,

(6)

где φ₀ - константа интегрирования, не зависящая от времени, и

(7)

это амплитуда фазовой модуляции, а ψ_n ‑ дополнительный сдвиг фазы модуляции относительно фазы сигнала φ_n , причем ctg ψ_n = ω_c / ω_n.

Итак, с учетом частотного чирпа электромагнитная волна (3) может быть представлена при малых глубинах амплитудной модуляции m<

.

(8)

Спектральный состав такой волны можно получить с помощью известного разложения Якоби-Ангера (Jacobi–Anger expansion) по функциям Бесселя [7]

.

(9)

В результате, для электромагнитной волны (8) приходим к следующему спектральному представлению

.

(10)

Видно, что спектр электромагнитной волны лазерного излучения с учетом чирпа содержит несущую частоту ω₀ и бесконечное количество боковых частот ω₀ + nω_m , где n = ±1,±2.±3..., сдвинутых влево и вправо с интервалом равным частоте модуляции ω_m.

 

Транспортировка оптического сигнала в одномодовом волокне

Как известно, электромагнитное поле моды оптического волокна имеет вид E = E₀(r,φ)e^i(ωt-βz), где β‑постоянная распространения волны с частотой ω (мы пренебрегаем затуханием). При одинаковом типе распределения электромагнитного поля в поперечном сечении волокна, E₀(r,φ), характерном для одномодового волокна, в нем могут распространяться волны с различной частотой. Хроматическая дисперсия этих волн, выражающаяся в зависимости постоянной распространения β от частоты ω, приводит к искажению сигнала на выходе из волокна.

В окрестности частоты несущей волны ω₀ функция β(ω) может быть представлена в виде степенного ряда [8]

,

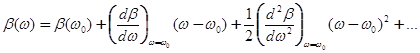(11)

где β₀ ‑ постоянная распространения на частоте несущей волны, коэффициент β₁=1/u равен обратной величине групповой скорости сигнала, u=dω/dβ, на частоте несущей волны и коэффициент β₂ определяется дисперсией групповой скорости волн в волокне. Он связан с, так называемым, коэффициентом дисперсии волокна D известным соотношением [8]

β2 = - λ02D/2πc,

(12)

где c – скорость света в вакууме, λ₀ ‑ длина волны излучения лазера. Типичные значения коэффициента D на длине волны 1550 нм составляют (16 ‑ 18) пс/(нм км).

При прохождении волокна длиной L каждая спектральная составляющая в (10) приобретает свой набег фазы равный -βL. Для волны с частотой ω₀+nω_n он составляет -βL=-β₀L-β₁nω_nL-(1/2)β₂n²ω_n²L - ... . Следовательно, на выходе из волокна имеем электромагнитную волну в виде

,

(13)

где

.

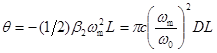(14)

 

Фототок приемника излучения

Фототок, регистрируемый детектором на выходе из волокна, пропорционален квадрату модуля напряженности электрического поля E(t) (13). Запишем фототок детектора в виде

,

(15)

где I(nω_m) ‑ комплексная амплитуда фототока гармоники с частотой nω_m. Используя при вычислении |E(t)||² = E(t)E*(t) теорему Графа о суммировании бесселевых функций (Graf's addition theorem) [7], получим в первом порядке по m выражение [9]

,

(16)

где

Un = 2M sin nΘ

(17)

и R ‑ чувствительность фотодетектора на длине волны излучения лазера.

Сравним фототок детектора на входе и на выходе из волокна. На входе в волокно L=0 и, следовательно, Θ (14) и U_n (17) тоже равны нулю. Учитывая тогда в (16) , что J₀(0)=1, а остальные функции Бесселя равны нулю в начале координат, приходим к выражению

.

(18)

Видно, что спектр фототока имеет вклад на нулевой частоте (постоянный ток) и на двух боковых частотах +ω_m и -ω_m. Как и ожидалось, фототок воспроизводит исходную модуляцию интенсивности излучения (2) и исходную токовую модуляцию (1).

На выходе из волокна фототок детектора (15) содержит вклад на нулевой частоте (постоянный ток) I(0)=RP₀ , а также, вообще говоря, и на всех частотах nω_m, где n=±1,±2,±3... . При этом сигнал приходит с запаздыванием на L/u , где u – групповая скорость. В частности, при n=1 имеем следующее выражение для комплексной амплитуды (16)

.

(19)

Сравнение (19) с соответствующей комплексной амплитудой сигнала частоты ω_m на входе в волокно, mRP₀/2 (18), дает выражение для передаточной функции сигнала по волокну длиной L на частоте модуляции ω_m:

.

(20)

Выделяя амплитуду и фазу передаточной функции (20), H(ω_m,L)=|H(ω_m,L)|e^iχ, запишем фототок (15) на частоте модуляции ω_m как

.

(21)

Видно, что модуль передаточной функции (20) определяет амплитуду сигнала детектора на выходе их волокна.

Рассмотрим некоторые частные случаи. Если частотного чирпа у лазерного источника нет (практически нереализуемый случай), то амплитуда фазовой модуляции M (7) равна нулю, и, следовательно, U1 =0. В этом случае модуль передаточной функция (20) равен |H(ω_m,L)| = |cosθ| [10, 11]. С учетом (14) тогда видно, что сигналы с частотами, определяемыми из условия θ = π/2 + lπ, где l = 0,1,2,3... , имеют на выходе из волокна амплитуду равную нулю.

При слабом чирпе и, следовательно, малых U₁ в степенных разложениях бесселевых функций в (20), можно ограничиться только первыми слагаемыми. Это можно сделать в области амплитуд фазовой модуляции, определяемой неравенством M² << 1. Такое требование заведомо выполняется при малых глубинах модуляции интенсивности, m<<1, и при частотах сигнала ω_m превышающих характеристическую частоту адиабатического чирпа ω_c (то есть при частотах сигнала больших нескольких ГГц). Это видно из выражения (7) с учетом типичных значений фактора Генри α, заключенных для современных полупроводниковых лазеров в пределах от 2 до 4. Модуль передаточной функции в этой области может быть записан в виде [6, 12, 13]

.

(22)

Типичный график зависимости 10 lg|H(ω_m,L)|² (то есть, график функции |H(ω_m,L)|² (22) выраженной в децибелах) от частоты модуляции f_m=ω_m/2π представлен на рисунке 1 для длины волокна L=10 км. При этом приняты следующие значения параметров чирпа α = 2, ω_c/2π = 2 ГГц и коэффициента дисперсии волокна D=16 пс/(нм км). Длине волны излучения лазера 1550 нм соответствует частота f₀ = ω₀/2π =193,414 ТГц.

Для экстремумов функции |H(ω_m,L)|² можно получить следующее аналитическое выражение

.

(23)

При заданной длине волока L это выражение вместе с (14) определяет в неявном виде частоту экстремумов мощности сигнала. С другой стороны, при заданной частоте модуляции ω_m соотношение (23) определяет длину волокна для экстремумов мощности сигнала на выходе. Как видно из рис. 1, для частот в области экстремумов выполняется неравенство (ω_c/ω_m)² << 1 и, поэтому, этим слагаемым в (23) можно пренебречь. В этом случае можно получить более простое выражение для определения экстремумов рассматриваемой функции, а именно θ = - arctg α + l π/2 с целыми положительными l, причем при нечетных l будут минимумы, а при четных l ‑ максимумы. Квадрат модуля передаточной функции в минимумах равен

,

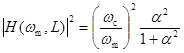(24)

а в максимумах

.

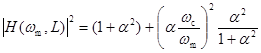(25)

Отметим также, что можно получить аналитические выражения для нулей функции на рис. 1 (в этих точках модуль передаточной функции (22) равен единице). Решение соответствующего тригонометрического уравнения содержит два набора корней: для нечетных нулей на рис. 1 имеем sin θ = 0 (откуда θ = lπ с целыми неотрицательными l), а для четных нулей получаем

.

(26)

Из графика на рис. 1 видно, что, также как и в формуле (23), слагаемым (ω_m/ω_m)² в (26) можно пренебречь. Тогда из соотношения (26) для четных нулей получаем условие θ = -2arctg α + lπ с целыми положительными l.

 

Нелинейные искажения сигнала

При больших плотностях мощности излучения в оптоволокне заметную роль начинают играть нелинейно-оптические явления, приводящие к нелинейным искажениям передаваемых сигналов. Причиной таких явлений является изменение свойств вещества под действием распространяющегося в нем света большой интенсивности. К наиболее существенным из них относятся [8]: вынужденное рассеяние Мандельштама-Бриллюэна (ВРМБ) (stimulated Brillouin scattering (SBS)); вынужденное комбинационное (рамановское) рассеяние (ВКР) (stimulated Raman scattering (SRS)); четырехволновое смешение (four-wave mixing (FWM)); фазовая автомодуляция (self-phase modulation (SPM)); и перекрестная фазовая модуляция (cross-phase modulation (CPM)). Влияние оптической нелинейности становится заметным при уровнях мощности излучения превышающих 10 мВт. В первую очередь это относится к ВРМБ, в то время как порог мощности для ВКР значительно выше и составляет примерно 1 Вт.

Дисперсия групповой скорости электромагнитных волн в оптоволокне приводит к нелинейным искажениям особого рода. Такие искажения не связаны мощностью транслируемого сигнала и имеют место даже при малых интенсивностях лазерного излучения. Действительно, сравним фототок детектора на входе и на выходе из волокна. Фототок детектора на входе в волокно, в соответствии с (18), является гармоническим электрическим сигналом на частоте ω_m . Как видно из выражения (15) с комплексной амплитудой (16), спектр фототока приемника излучения на выходе из волокна содержит, кроме гармоники на частоте сигнала ω_m, также и высшие гармоники этой частоты. Другими словами, при транспортировке сигнала по волокну возникают его нелинейные искажения.

Важно подчеркнуть, что мы рассматриваем среду оптоволокна как линейную, а причиной нелинейных искажений является дисперсия групповой скорости электромагнитных волн. При этом наличие (вследствие частотного чирпа) в спектре входящей электромагнитной волны (10), кроме несущей частоты ω_m, бесконечного количества боковых частот ω₀ + nω_n , где n = ±1,±2,±3... , еще не означает нелинейности сигнала фототока. Фазовые соотношения между спектральными компонентами во входящей электромагнитной волне (10) таковы, что фототок детектора (18) является гармоническим электрическим сигналом. При транспортировке сигнала по волокну вследствие дисперсии возникают дополнительные фазовые сдвиги боковых частот относительно несущей, из-за чего в электромагнитной волне (13) на выходе диспергирующего волокна спектральные компоненты сигнала складываются в иных, по сравнению с входящей электромагнитной волной (10), фазовых соотношениях. В результате, фототок детектора на выходе из волокна приобретает нелинейные искажения. Принципиальным отличием дисперсионных нелинейных искажений является то, что они возникают в спектре огибающей электромагнитной волны, а не в спектре несущей, как это было бы при распространении волн через нелинейную среду.

Интересно отметить, что в нечетных нулях функции 10lg|H(ω_m, L)|² на рис. 1, когда sin θ = 0 (откуда θ = lπ с целыми неотрицательными l), все комплексные амплитуды (16), кроме первой с n=1, обращаются в ноль. Таким образом, трансляция гармонических сигналов с частотами, определяемыми из соотношения

,

(27)

где l = 1,2,3... , не сопровождается нелинейным искажениям. При этом, модуль передаточной функции для сигналов с частотой (27) равен единице и, следовательно, амплитуды сигнала фототока детектора на входе и на выходе из волокна в точности равны друг другу (без учета затухания в волокне). Необходимо, однако, учесть, что неравномерность амплитудно-частотной характеристики (см. рис. 1) в окрестности частот (27) оказывается максимальной и в этой области будут наибольшие линейные искажения сигнала. Для параметров ВОЛС, использованных при построении графика на рис. 1, получаем следующую оценку f_m1= ω_m1 /2π = 27,93 ГГц и f_m2 = 39,49 ГГц.

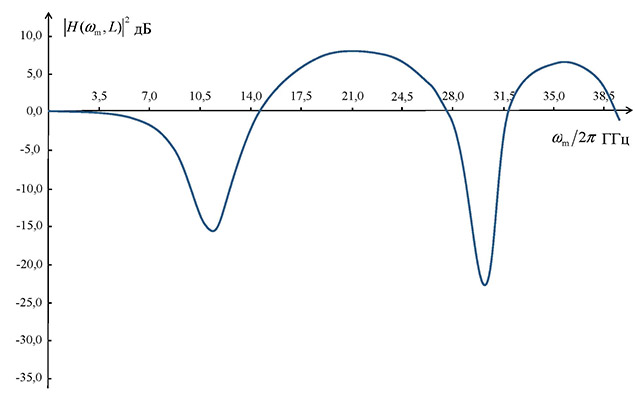
Рис. 1. График квадрата модуля передаточной функции |H(ω_m, L)|² (22) (выраженной в децибелах) от частоты модуляции f_m = ω_m/2π. Длина оптоволокна L=10 км, коэффициент дисперсии волокна D=16 пс/(нм км), длина волны излучения лазера 1550 нм, параметры частотного чирпа: α = 2, f_c = ω_c/2π = 2 ГГц.

 

Обычно, основной вклад в нелинейные искажения сигнала фототока дают вторая и третья гармоники. При определенных частотах входного сигнала вклады этих гармоник пропадают. Действительно, как видно из (16) комплексная амплитуда второй гармоники обращается в ноль при sin 2θ = 0 (откуда θ = lπ/2 с целыми неотрицательными l), а для третьей гармоники аналогичное условие выглядит как sin 3θ = 0 (откуда θ = lπ/3 с целыми неотрицательными l). Для параметров ВОЛС, использованных при построении графика на рис. 1, получаем следующую оценку: f_m1⁽²⁾ = ω_m1 ⁽²⁾/2π = 19,75 ГГц и f_m2⁽²⁾ = 27,93 ГГц (при этих частотах пропадает вторая гармоника) и f_m1⁽³⁾ = ω_m1⁽³⁾/2π = 16,13 ГГц и f_m2⁽³⁾ = 22,80 ГГц (при этих частотах пропадает третья гармоника).

Из рис. 1 видно, что наиболее привлекательной областью функционирования ВОЛС с рассматриваемыми параметрами является область частот 19÷23 ГГц. В этой области частот преобразование модулированного электрического сигнала в оптический происходит с относительно небольшими нелинейными искажениями. В этой области происходит дисперсионное увеличение мощности сигнала на частоте модуляции на выходе из волокна. Эта область характеризуется относительно небольшими линейными искажениями сигнала. Наконец, в этой области лежат частоты модуляции, при которых в выходном сигнале фототока пропадает вторая и третья гармоники (f_m1⁽²⁾ = 19,75 ГГц и f_m2⁽³⁾ = 22,80 ГГц, соответственно) и, следовательно, можно минимизировать нелинейные искажения сигнала.

 

Экспериментальные данные

Полученный экспериментально график зависимости отношения (выраженного в децибелах) мощности сигнала на выходе из волокна к мощности входного сигнала от частоты модуляции f_m = ω_m/2π представлен на рис. 2 для нескольких отрезков одномодового оптоволокна с коэффициентом дисперсии волокна D = 16 пс/(нм км). Используется InGaAsP лазер с распределенной обратной связью (distributed feedback (DFB) laser) с длиной волны излучения 1550 нм.

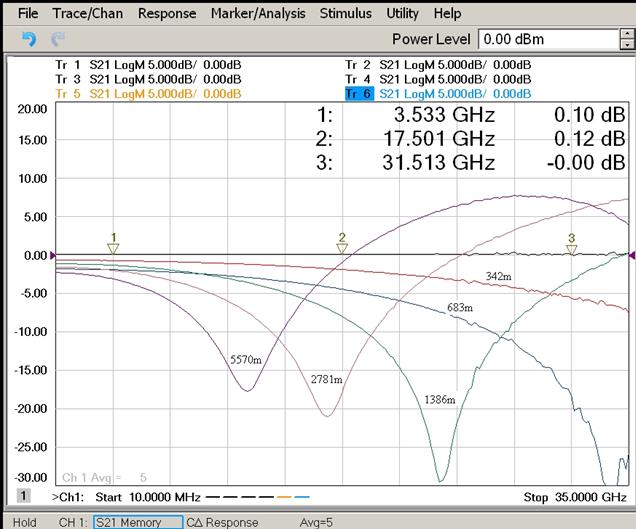
Рис. 2. Экспериментальный график зависимости отношения (выраженного в децибелах) мощности сигнала на выходе из волокна к мощности входного сигнала от частоты модуляции f_m = ω_m/2π для нескольких отрезков одномодового оптоволокна длиной 5570 м, 2781 м, 1386 м, 683 м и 342 м. Коэффициент дисперсии волокна D= 16 пс/(нм км), используется DFB InGaAsP лазер с длиной волны излучения 1550 нм.

 

Видно качественное согласие с теоретической кривой, приведенной на рис. 1. Провалы мощности сигнала наблюдаются при частотах f_m = 12,2 ГГц для длины волокна L=5570 м, глубина провала ‑ 17,5 дБ; f_m = 16,3 ГГц для длины волокна L=2781 м, глубина провала ‑ 21,0 дБ; f_m = 23,5 ГГц для длины волокна L=1386 м, глубина провала ‑ 28,5 дБ.

Широкий максимум мощности сигнала наблюдается в области 28,0÷28,2 ГГц для длины волокна L=5570 м, увеличение мощности сигнала составляет +7,5 дБ.

Количественное соответствие можно установить, используя выражение для частот экстремумов мощности сигнала

(28)

где l=1,2,3... , причем при нечетных l будут минимумы, а при четных l ‑ максимумы. С помощью (28) получаем следующую оценку для фактора Генри α=2,9. Значение квадрата модуля передаточной функции в минимумах (24) и максимумах (25) позволяет теперь определить характеристическую частоту f_c адиабатического чирпа. Наилучшее совпадение с расчетными значениями дает f_c = ω_c/2π =1,7 ГГц.

Следует отметить, что производители лазеров не указывают параметров чирпа. Приведем для справки данные работы [14] для DFB лазеров с длиной волны λ₀ = 1550 нм с прямой токовой модуляцией интенсивности излучения: α= 2,8 ± 0,2 и k = (11,4 ± 0,5) с^‑1 мВт^‑1 (при мощности излучения P₀ =1мВт это дает f_c = kP₀/2π = 1,8 ГГц). Видно, что имеется хорошее количественное согласие с результатами нашего расчета.

Заключение

В данной работе последовательно рассмотрены все этапы прохождения сигнала в аналоговой ВОЛС с прямой токовой модуляцией интенсивности и прямым детектированием фототока на выходе из оптоволокна. Показано, что эффект частотного чирпа лазерного излучения и хроматическая дисперсия оптоволокна оказывают существенное влияние на результат трансляции сигнала. Получено выражение для передаточной функции, связывающей фототок детектора на частоте модуляции после и до транспортировки сигнала в диспергирующем волокне. В частных случаях полного отсутствия частотного чирпа и слабого частотного чирпа получены более простые выражения для передаточной функции, совпадающие с установленными ранее на начальных стадиях исследования этого вопроса. Получены простые аналитические выражения для частот сигналов с минимальной или с максимальной мощностью на выходе из волокна заданной длины. Получены простые аналитические выражения для частот, в окрестности которых следует ожидать наибольших линейных искажений сигнала. Выполнено сравнение рассчитанной передаточной функции с аналогичной функцией полученной экспериментально и установлено удовлетворительное количественное согласие между ними.

Подробно исследованы дисперсионные нелинейные искажения сигнала. Установлено, что такие искажения не связаны с мощностью транслируемого сигнала и имеют место даже при малых интенсивностях лазерного излучения. Получены простые аналитические выражения для частот, при которых не будет дисперсионных нелинейных искажений. Получены также простые аналитические выражения для частот, при которых в выходном сигнале пропадают вторая или третья гармоники, то есть те гармоники, которые обычно вносят основной вклад в дисперсионные нелинейные искажения сигнала фототока. Даны рекомендации по выбору оптимального частотного диапазона функционирования ВОЛС с прямой модуляцией интенсивности и прямым детектированием сигнала фототока на выходе из оптоволокна.

 

Список литературы

1. Ривлин Л.А. Динамика излучения полупроводниковых квантовых генераторов (М.: Советское радио, 1976).

2.  Полупроводниковые инжекционные лазеры. Динамика, модуляция, спектры. (пер. с англ. под ред. У. Тсанг, М.: Радио и связь, 1990). (Semiconductors and Semimetals. Volume 22: Lightwave Communications Technology, Semiconductor Injection Lasers, Part 1, ed. by W.T. Tsang, New York: Academic Press, 1985)

3.  Koch T.L., Bowers J.E. Electronics Letters, 20, 1038 (1984).

4.  Agrawal G.P., Dutta N.K. Long-wavelength Semiconductor Lasers (New York: Van Nostrand Reinhold, 1993).

5.  Petermann K. Laser Diode Modulation and Noise (Dordrecht: Kluwer Academic Publishers, 1988).

6.  Bjerkan L., Royset A., Hafskjaer L., Myhre D. Journal of Lightwave Technology, 14, 839 (1996).

7.  Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены. (М: Наука, 1966, гл. 7.2.4, гл. 7.6.2). (Bateman H., Erdelyi A. Higher Transcendental functions, v. 2 (New York: Mc Graw-Hill book company, 1953, Ch. 7.2.4, Ch. 7.6.2)).

8.  Agrawal G.P. Nonlinear Fiber Optics (New York: Academic Press 2013, 5th edition, ch. 1).

9.  Peral E., Yariv A. Journal of Lightwave Technology, 18, 84 (2000).

10. Meslener G.J. IEEE J. Quantum Electron., 20, 1208 (1984).

11. Wang J., Petermann K. Journal of Lightwave Technology, 10, 96 (1992).

12. Royset A., Bjerkan L., Myhre D., Hafskjaer L. Electron. Lett., 30, 710 (1994).

13. Srinivasan R.C., Cartledge J.C. IEEE Photon. Technol. Lett., 7, 1327 (1995).

14. Villafranca A., Lasobras J., Garcés I. In Proceedings of 6th Spanish Conference on Electronic Devices (San Lorenzo de El Escorial, Madrid, Spain 2007, p. 173).

 

Dispersive distortions of a signal in analog fiber-optical links with direct intensity modulation

V.V. Shcherbakov¹, A.F. Solodkov¹, A.A. Zadernovsky²

¹JSC «Center VOSPI», Vvedenskogo St., 3, Moscow 117342, Russia

²Moscow State University of Information Technologies, Radioengineering and Electronics, Vernadskogo Аv., 78, 119454, Russia

We have considered consecutively all the stages of signal propagation in an analog fiber-optical link with direct intensity modulation and direct detection of photocurrent output of the fiber. It has been shown that the frequency chirping of laser radiation and the group velocity dispersion of electromagnetic waves in the optical fiber make a significant impact on the signal transmission. The output signal reveals ether power fading or power gain depending on the modulation frequency. We have derived simple analytical expressions for the frequencies of the signals with minimum or with maximum power at the output of a fiber of a given length. We have examined dispersive harmonic distortions of the signal. It has been shown that such harmonic distortions are not related to a power of the transmitted signal and occur even at low laser light intensities. We have derived simple analytical expressions for the frequencies at which there will be no dispersive harmonic distortions. We have also derived simple analytical expressions for the frequencies at which the output signal does not contain second or third harmonic that is the harmonics that usually make a majo